The quest to build an AI capable of advanced mathematical reasoning has hit a major milestone. Researchers behind the new AlphaProof system, detailed in a paper published in Nature, have demonstrated an AI capable of solving problems from the notoriously difficult International Mathematical Olympiad (IMO), achieving a silver medal performance in the 2024 contest.
The AlphaProof system, developed by Julian Schrittwieser and colleagues while at Google DeepMind, successfully generated formal proofs for three of the six IMO problems (P1, P2, and P6). Crucially, P6 was considered the hardest problem of the contest, solved by only five out of 609 human participants. This achievement isn't just about solving hard math; it’s about solving it with guaranteed, verifiable truth, bypassing the hallucination issues plaguing general-purpose large language models (LLMs).
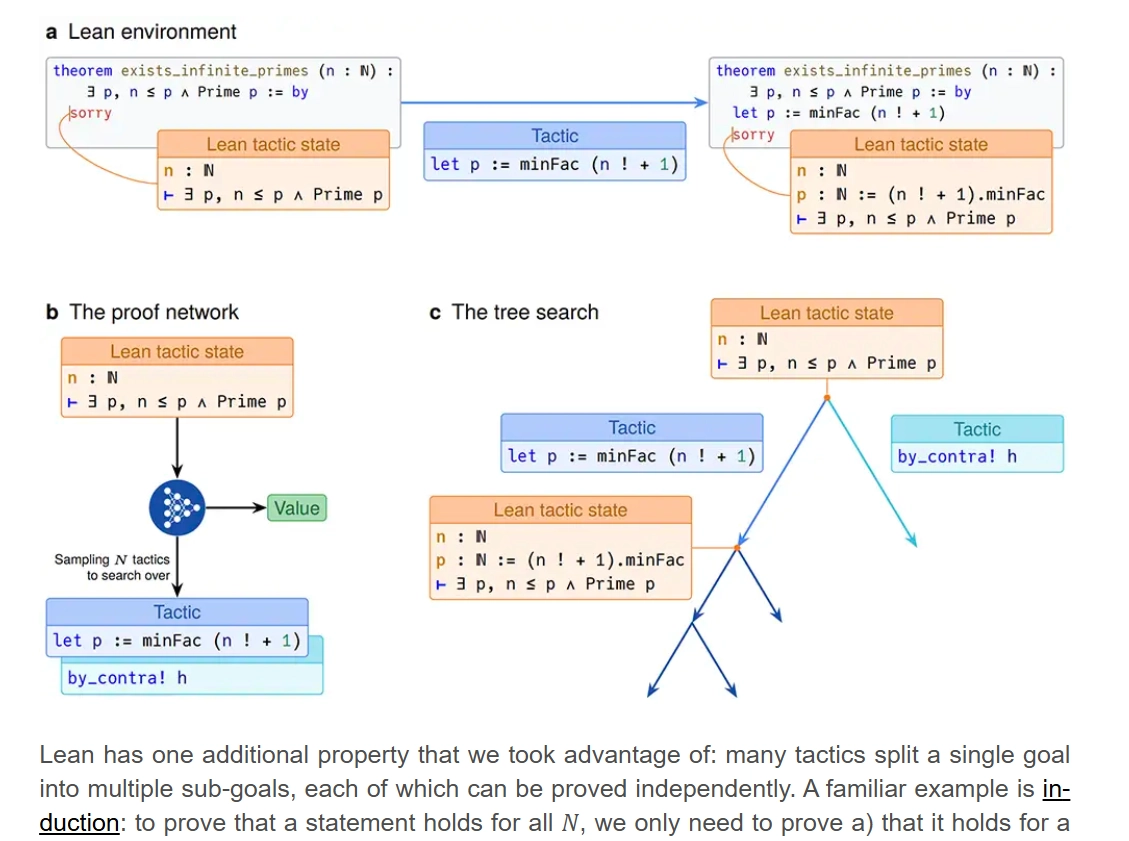
Unlike systems that output proofs in natural language—which still require human mathematicians to manually verify every step—AlphaProof operates entirely within Lean, a formal proof assistant language. Lean’s structure is ideal for programmatic discovery: proofs are composed of short, verifiable “tactics,” and the system can automatically check if the final result is logically sound, making it perfect for Reinforcement Learning (RL) reward computation.
The system’s foundation is a massive encoder-decoder transformer, pretrained for an unprecedented 50 epochs on a mix of code and mathematical data, seeing 12 trillion tokens on the encoder side. This specialized training ensures the model can generate plausible Lean tactics from the start.
Why Formal Verification Changes Everything
The real innovation lies in how AlphaProof leverages AlphaZero-style tree search and RL to navigate the vast space of possible proofs. Because Lean proofs often involve splitting a single goal into multiple independent sub-goals (like induction), the team introduced a new concept into the search algorithm: the "product node." This node requires all its children to be proven, allowing the search to efficiently track which sub-goals are complete and focus compute on the hardest remaining branches.
To scale the RL training, the team had to overcome the limited size of existing formal proof libraries (like Lean’s mathlib). They trained a second network to formalize 1 million natural language theorem statements into 80 million distinct Lean statements. This massive, synthetic dataset allowed for extensive RL training, where the system learned to optimize for shorter, more elegant proofs.
For the final IMO challenge, the researchers employed a technique called Test-Time RL. Instead of simply running the trained model, they used an LLM to generate many variations of the target theorem (like IMO P6). This created a natural curriculum, where solving easier variants provided insights and stepping stones toward solving the main, complex problem. This demonstrates the scalability of investing significant compute at the moment of inference to obtain superior, verifiable results.
The implications extend far beyond competitive mathematics. AlphaProof represents a significant step toward reliable, high-stakes AI reasoning. By producing outputs in a formal language that can be automatically verified, the system eliminates the need for human trust or manual checking, even for the most complex mathematical statements. As the researchers note, this success shows that the principles of RL combined with search work just as well for LLMs, opening the door for more general, verifiable AI systems in science and engineering.
Julian Schrittwieser, formerly of Google DeepMind, detailed the AlphaProof system on his blog following the publication of the full paper, Olympiad-Level Formal Mathematical Reasoning with Reinforcement Learning, in Nature.